we're going to begin looking at Epsilon Delta proofs for limits. The limits contain a couple of variables that need introducing.
Variable number one:
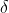
That character has one of two names. Funny looking d thing and delta. The cool kids call it delta.
Variable number two:

This one could either be fratty e or epsilon. We're going with the latter.
So, we have Epsilon and Delta, now we need to know what they're good for. We'll start by reviewing the following equation:

In Math speak, we should read: The limit of

as
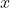
approaches

is equal to
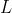
. That's all well and good, but how do we know the equation is true? That's where

and
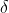
come in. Consider the following equation:

This can be read as if
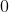
is less than the absolute value of

which is less than
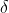
, then the absolute value of

is less than

. On it's own, the equation means nothing, but we're going to apply it to what we know about limits. Specifically:

This should look somewhat familiar. The part that may be new is

which simply means if and only if. Looking at our new equation, we're theorizing that the limit of

as
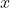
approaches

is equal to
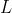
if and only if for every value of
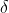
which meets the inequality

, there exists a value for

which meets the inequality

.
This is admittedly a mouth full. It may take some time to wrap your head around, but it's not an overtly difficult concept once you mull it over for a while. The underlying concept is that when
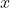
is within
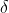
units of

,

must be within

units of
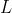
for the limit to exist. Extrapolating on that idea we can deduce that if we find a value of
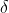
for which both inequalities are true, then the inequalities will be true for all values between
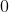
and
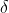
as long as we adjust

proportionately. Thus to prove a limit is true using the Epsilon-Delta method, we must find a way to relate

and
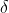
.
The next post will go through some examples using this method to help flush out these somewhat abstract ideas.
No comments:
Post a Comment